つい最近、東海オンエアが公開していた
『1/1024』と『1/2を10回連続(1/1024)』ってどっちの方が確率高いの!?【数学革命シリーズ】
が面白かったので、勝手にガチ検証した。
内容としては、タイトルの通り1/1024 と1/2を10回連続当てるのはどちらが確率高いという内容だが、実際に同様に何かしらの差は生まれるのか、プログラムで検証してみた。
検証の方法としては
- 文系の検証では1,2をランダムで返す変数を用意して1が10回連続で返された場合を一回とする。
- 理系の検証では1~1024のランダムな整数値を返す変数を用意して変数の値が634の場合を一回とする。
- それぞれ,100回になるまで、繰り返し平均を取る。
- もちろん、ランダムの確率は同様に確か。
- 平均の値が低い方が確率が高いと結論づける。
こんな感じで検証していきます。
ソースコード
処理自体はかなり簡単、プログラミングの最初の課題とかに、もってこいのちょうど良いレベル笑
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 |
import random import math import statistics import matplotlib.pyplot as plt print(random.randint(1,1024)) rand_sci = random.randint(1,1024) check_hum = 1 check_sci = 643 #試行回数 10000 count_hum = 0 count_sci = 0 #一セット何回試行したか end_list_hum = [] end_list_sci = [] while count_hum < 100: try_hum = 0 try_prob = 0 while try_prob < 9: try_hum += 1 rand_hum = random.randint(1,2) if (rand_hum == check_hum): try_prob += 1 else: try_prob = 0 # print(try_prob) end_list_hum.append(try_hum) count_hum += 1 while count_sci < 100: try_prob = 0 try_sci = 0 while try_prob < 1: rand_sci = random.randint(1,1024) try_sci += 1 if (rand_sci == check_sci): count_sci += 1 end_list_sci.append(try_sci) try_prob +=1 print(statistics.mean(end_list_hum)) print(end_list_hum) print(statistics.mean(end_list_sci)) num = [i+1 for i in range(100)] plt.scatter(num,end_list_hum) plt.scatter(num,end_list_sci) plt.show() |
検証結果
オレンジ:文系
平均値:1072.51
青:理系
平均値:857.87
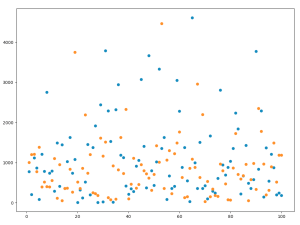
ガチ検証結果的には、1/1024の方が確率が高いという結果になりました笑
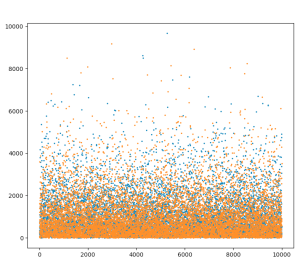
ちなみに、試しに試行回数10000で実行すると以下のような結果になりました。
オレンジ:文系
平均値:1018.05
青:理系
平均値:10.20.67
文系が僅かに勝ってますが、当然のように両者収束しています笑
最後に
いかがだったでしょうか。
お察しの結果通りだったと思います。
てつやの発想力が天才なのと
この内容を面白い動画に昇華にできる東海オンエアすげーってことが分かりました。
動画面白いので見ましょう。以上です。

コメント